机器人的现代数学知识(Lie Groups)¶

参考：
paper: A micro Lie theory for state estimation in robotics
lib: manif
lib: sophus
book:《Modern Robotics Mechanics, Planning, and Control》Kevin M. Lynch, Frank C. Park (讲解视频) book:《机器人学的现代数学理论基础》丁希仑
videos: 南科大

1 基础知识¶

frame (physics) coordinate systems (mathematics)

自由向量（free vector）

geometric quantity with length and direction

无坐标的（coordinate free）

$p$ denotes a point in the physical space
A point $p$ can be represented by a vector from frame origin to $p$
${}^Ap$ denotes the coordinates of point $p$ wrt frame $A$
When left-superscript is not present, it means the physical vector itself or the coordinates of the vector for which the reference frame is clear from the context.

反对称矩阵（skew-symmetric） $$ w=[w_1,w_2,w_3]^T $$

\[ [w]= \begin{bmatrix} 0 & -w_3 & w_2 \\ w_3 & 0 & -w_1 \\ -w_2 & w_1 & 0 \end{bmatrix} \]

\[ [w]=-[w]^T \]

$[w]$ is called a skew-symmetric matrix representation of the vector $w$

有的也用 $\hat{w}$ 表示 skew-symmetric

$a \times b = [a]b$: cross product 本质上对后面这个vector进行了一个线性变换

旋转矩阵(Rotation Matrix) Frame: 3 coordinate vectors(unit length) $\hat{x}, \hat{y}, \hat{z}$ and an origin

$\hat{x}, \hat{y}, \hat{z}$ mutually orthogonal
$\hat{x} \times \hat{y} = \hat{z}$, right hand rule

Rotation matrix: specifies orientation of one frame relative to another

\[{}^AR_B = [{}^A\hat{x}_B, {}^A\hat{y}_B, {}^A\hat{z}_B] \]

where, ${}^A\hat{x}_B$ 是$\hat{x}_B$在A frame下的coordinate

\[R \in \mathbb{R}^{3 \times 3}\]

Properties:

\[ R^TR^{-1} =I \]

\[ R^{-1} = R^T\]

根据后面李群的知识：$\(R \in SO(3)$\)

齐次变换矩阵

\[T=(R,p) \in \mathbb{R}^{4 \times 4}\]

根据后面李群的知识：$\(T \in SE(3)$\)

欧式空间、非欧空间

欧式空间：距离、面积、体积等
非欧空间：黎曼几何、曲率等

角速度（angular velocity） $$ w= \hat{w} \dot{\theta} $$

$\hat{w}$ 表示单位转轴（unit vector），$\dot{\theta}$表示角速度（scalar）

2 群¶

问题：为什么会引入群这个概念？回答：

看这个视频总结的

群是 一种集合 + 一种运算 的代数结构：记集合为$A$，运算为$\cdot$，当运算满足封闭性 Closure、结合率 Associativity、幺元 Identity element、逆 Inverse element四条性质，称$(A,\cdot)$为群

群的4个基本性质：封闭性、结合律、幺元律、可逆性

交换群(commutative group)、阿贝尔群(Abelian group)

旋转矩阵集合 + 矩阵乘法构成群 $\to$ 三维特殊正交群/旋转矩阵群$SO(3)$
变换矩阵集合 + 矩阵乘法构成群 $\to$ 三维特殊欧式群/变换矩阵群$SE(3)$
常见的其他群
一般线形群$GL(n,\mathbb{R})$: $n\times n$的可逆（非奇异）实矩阵（二元运算：矩阵乘法），也可以记作: $GL(n)$
特殊正交群$SO(n)$: $n\times n$的单位正交实数矩阵（二元运算：矩阵乘法），$SO(2)$、$SO(3)$是两个比较重要的子群。
特殊欧式群$SE(n)$: 三维特殊正交群$SO(3)$和向量空间$\mathbb{R}^3$的半直积为特殊欧式群$SE(3)$: $SE(3)=SE(3)\otimes \mathbb{R}^3$，$SE(3)$也是特殊欧式群的一个子群。

3 李群¶

3.1 李群¶

李群：群的4个基本性质+3个特殊条件（可微流形、群的积是可微分的映射、群的逆也是可微分的映射）

一般意义的李群指的的乘法，不是加法。即矩阵李群。

典型例子： - $n$维向量空间 $\mathbb{R}^n$ - 单模复数群 $z = \cos\theta + i\sin\theta$ - 一般线性群 $GL(n,\mathbb{R})$ - $n\times n$ 非奇异实数矩阵 - 正交群 $O(3)$ - $n\times n$ 正交实数矩阵 - 特殊正交群 $SO(n)$ - $n\times n$ 单位正交实数矩阵 - 三维旋转群 $SO(3)$ - 三维特殊欧式群 $SE(3)$ - 幺模群 - 特殊幺模群

3.1 李子群¶

组合运算 composition

直积direct product
半直积semi-direct product

交运算 intersection

李子群的交集还是李子群

商运算 quotient

4 李代数¶

4.1 李代数¶

李代数对应李群的正切空间，它描述了李群局部的导数。

李群：大写，例如$SE(3)$，$SO(3)$ 李代数：小写，例如$se(3)$，$so(3)$

$SE(3)$的李代数是$se(3)$
$SO(3)$的李代数是$so(3)$

李群表示刚体运动、李代数表示刚体运动速度，李群和李代数是指数映射关系。

4.2 指数映射¶

4.3 伴随表达¶

5 李括号¶

6 总结¶

6.1 SE(3)、SO(3)、se(3)、so(3)¶

1、$3 \times 3$ 旋转矩阵组成的集合称为特殊正交群（special orthogonal group）$SO(3)$

特殊正交群$SO(3)$称为旋转矩阵群
特殊正交群$SO(2)$是所有$2 \times 2$实数矩阵的集合，二维的

2、特殊欧氏群（special Euclidean group）$SE(3) $，称为刚体运动群、齐次变换矩阵（homogeneous transformation matrice）群

刚体的位形空间可以表示为$SO(3)$与$\mathbb{R}^3$的乘积空间（半直积）记作$SE(3)$

\[ SE(3) = SO(3) \otimes \mathbb{R}^3\]

3、大写是李群、小写是李代数；他们之间是指数映射的关系；如下面两个exp的关系；

针对刚体运动，无论齐次坐标表达，还是伴随表达，都是具有指数映射关系$A=e^{\theta S}$;$Ad(g)=e^{\theta ad(j)}$

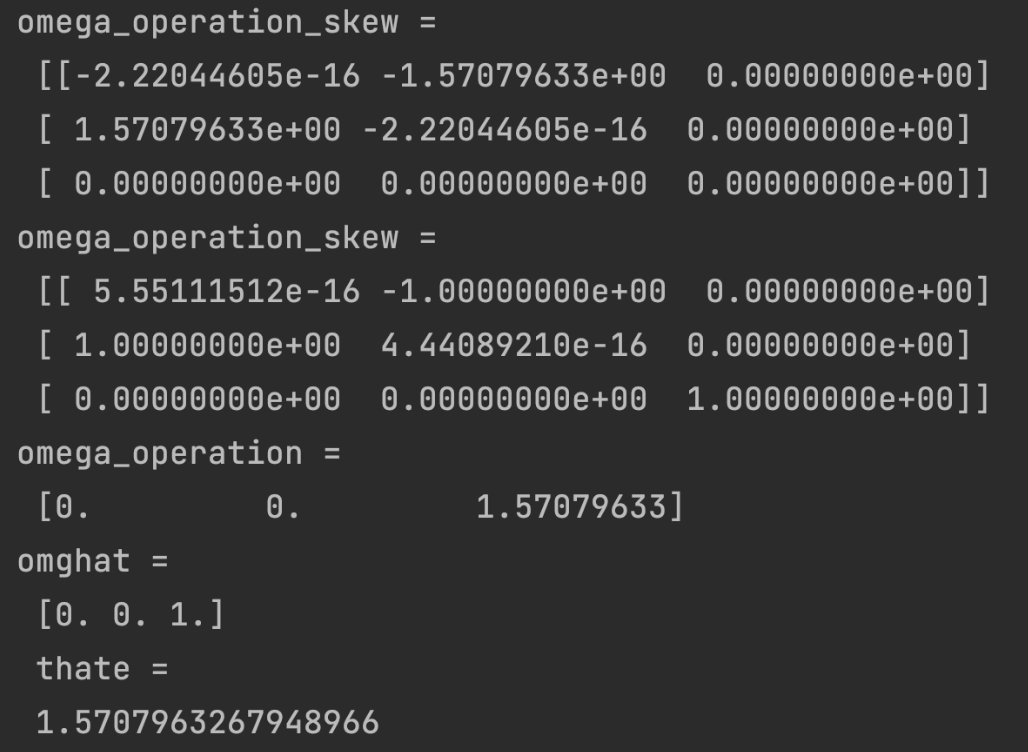
4、所有$3 \times 3$反对称矩阵的集合称为$so(3)$，$so(3)$是三维旋转群的李代数 For any unit vector $[\hat w] \in so(3)$ and any $\theta \in \mathbb{R}$ $$ e^{[\hat w]\theta} \in SO(3)$$

For any $R \in SO(3)$,there exists $[\hat w] \in \mathbb{R^3}$ with $||\hat w||=1$ and $\theta \in \mathbb R$ such that $$ R=e^{[\hat w]\theta} $$

\[exp:[\hat w]\theta \in so(3) \to R \in SO(3)\]

\[log:R \in SO(3) \to [\hat w]\theta \in so(3)\]

The vector $\hat w\theta \in \mathbb{R^3}$ is called the exponential coordinate for $R$

Python
import packages.Python.modern_robotics.core as mr
import numpy as np
from scipy.linalg import expm, logm

R = np.array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])

omega_operation_skew = logm(R)
print('omega_operation_skew = \n', omega_operation_skew)
R_test = expm(omega_operation_skew)
print('omega_operation_skew = \n', R_test)

omega_operation = mr.so3ToVec(omega_operation_skew)
print('omega_operation = \n', omega_operation)
omghat, thate = mr.AxisAng3(omega_operation)
print('omghat = \n', omghat, '\n', 'thate = \n', thate)

结果如下所示：

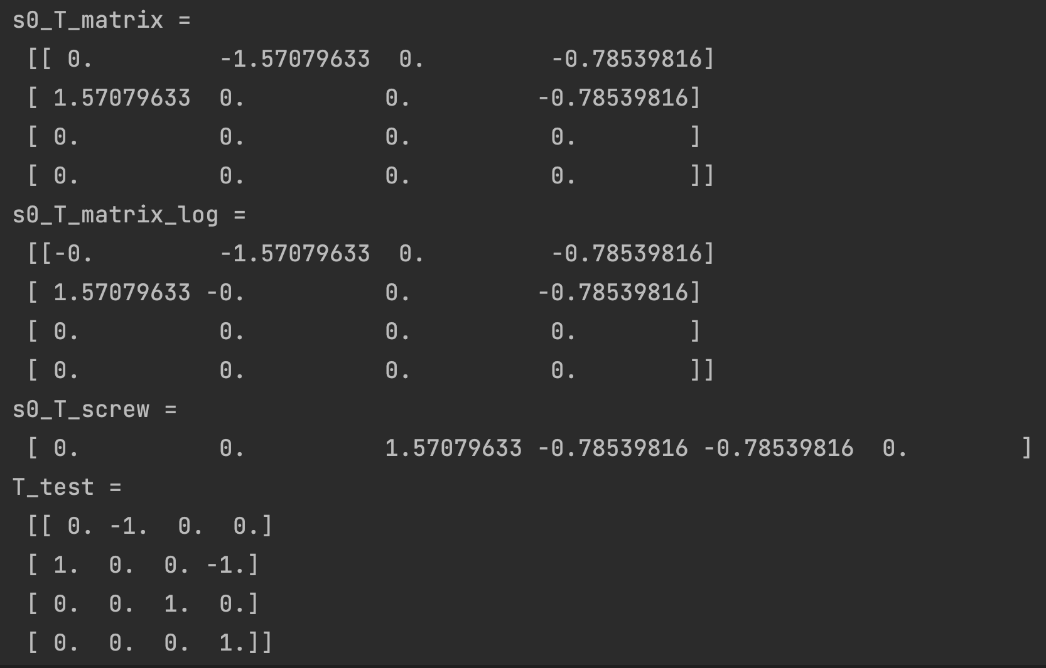
Rodrigues'Formula: Given any unit $[\hat w] \in so(3)$,we have $$ e^{[\hat{w}\theta]} = I + [\hat{w}]sin(\theta)+ [\hat{w}]^2(1-cos(\theta))$$

证明：将指数按照幂级数展开，再结合$sin(\theta)$和$cos(\theta)$的展开，化简。

刚体运动的指数坐标

\[exp:[\mathcal{S}]\theta \in se(3) \to T \in SE(3)\]

\[log:T \in SE(3) \to [\mathcal{S}]\theta \in se(3)\]

矩阵指数$e^{\mathcal{S} \theta}$

\[ e^{[\mathcal{S}]\theta} = \begin{bmatrix} e^{[w]\theta} & G(\theta)v\\ 0 & 1 \end{bmatrix} \]

\[G(\theta)=I\theta+(1-cos\theta)[w]+(\theta -sin\theta)[w]^2\]

Python
import packages.Python.modern_robotics.core as mr
import numpy as np
from scipy.linalg import expm, logm
np.set_printoptions(suppress=True)

T = np.array([[0, -1, 0, 0], [1, 0, 0, -1], [0, 0, 1, 0], [0, 0, 0, 1]])

s0_T_matrix = mr.MatrixLog6(T)
print('s0_T_matrix = \n', s0_T_matrix)
s0_T_matrix_log = logm(T)
print('s0_T_matrix_log = \n', s0_T_matrix_log)
s0_T_screw = mr.se3ToVec(s0_T_matrix)  # 得到Twist
print('s0_T_screw = \n', s0_T_screw)
T_test = expm(s0_T_matrix)
print('T_test = \n', T_test)

结果如下：

6.2 不同表达、不同运算¶

不同表达对应不同的运算，各有各的好处。

伴随表达也具有指数映射的关系$Ad(j)=e^{\theta ad(j)}$

3×3表达的旋转运动的李群$T$和其对应的李代数

\[ R \in SO(3) \]

\[ [w] \in so(3) \]

\[ R = e^{\theta \mathcal{[w]}} \]

齐次坐标表达的刚体运动的李群$T$和其对应的李代数

\[ T = \begin{bmatrix} R & p \\ 0 & 1 \end{bmatrix}_{4\times4} \in SE(3) \]

\[ S = \begin{bmatrix} [w] & v \\ 0 & 0 \end{bmatrix}_{4\times4} \in se(3) \]

\[ T = e^{\theta \mathcal{S}} \]

\[ T^{-1} = \begin{bmatrix} R^T & -R^Tp \\ 0 & 1 \end{bmatrix} \]

伴随表达（adjoint rspresentation）的刚体运动的李群$Ad_T$和对应的李代数

\[ Ad_T= \begin{bmatrix} R & 0 \\ [p]R & R \end{bmatrix}_{6\times6}\]

\[ ad_T= \begin{bmatrix} [w] & 0 \\ [v] & [w] \end{bmatrix}_{6\times6}\]

\[ Ad_T = e^{\theta ad_T}\]

$Ad_T$ 也可以表示成 $Ad(g)$

7、旋量理论与机器人运动学¶

所有的刚体运动都可以用螺旋运动表示。

旋量是一条有节距的直线；当节距=0，旋量$\to$线矢量。

7.1、齐次坐标与线矢量¶

点的齐次表示

面的齐次表示

线的齐次表示

Plucker坐标

线几何（线矢量）：

线矢量（line vector）：依附在空间某一直线上的向量（p29，戴建生）

\[ S=(s;s_0)=(s;r\times s)=(L,M,N;P,Q,R) \]

$s$称为原部矢量，$s_0$称为偶部矢量

线矢量，点乘没有意义；不过可以计算代数和、互易积（reciprocal product）

7.2、旋量、螺旋运动¶

如果是4×4表达，利用共轭运算conjunction，可以进行刚体变换：$T = T_2T_1T_2^{-1}$
如果是伴随表达，即4×4，共轭运算和伴随表达是等价的，即：

Twist / Spatial vector（运动旋量）、screw motion（螺旋运动）

\[ \mathcal{V}_b = \begin{bmatrix} w_b \\ v_b \end{bmatrix} \]

\[ \mathcal{V}' = [Ad_T]\mathcal{V} \]

运动旋量写成矩阵的形式 $$ [\mathcal{V}_b] = \begin{bmatrix} [w_b] & v_b \ 0 & 0 \end{bmatrix} \in se(3)$$

运动旋量 $\mathcal{V}$ 可以写成螺旋轴（screw axis）$\mathcal{S}$与绕该轴转动的速度的组合形式

1、Consider “unit velocity” $\mathcal{V} = \mathcal{S}$
2、if not unit speed $\mathcal{V} = \mathcal{S}\dot \theta$
3、$\mathcal{V} = ScrewToTwist(\hat w,h,q,\dot \theta)=ScrewToTwist(\hat w,h,q,\dot \theta=1)\dot \theta$

screw motion $$ \mathcal{V} = [w;v]=[\hat{s}\dot{\theta};-\hat{s}\dot{\theta}\times q+h\hat{s}\dot{\theta}]=[-w \times q+hw] $$

7.3、Forward Kinematics¶

参考：

calculation of the configuration（pose） $T=(R,p)$ of the end-effector frame from joint variables $\theta =(\theta_1,...,\theta_n)$

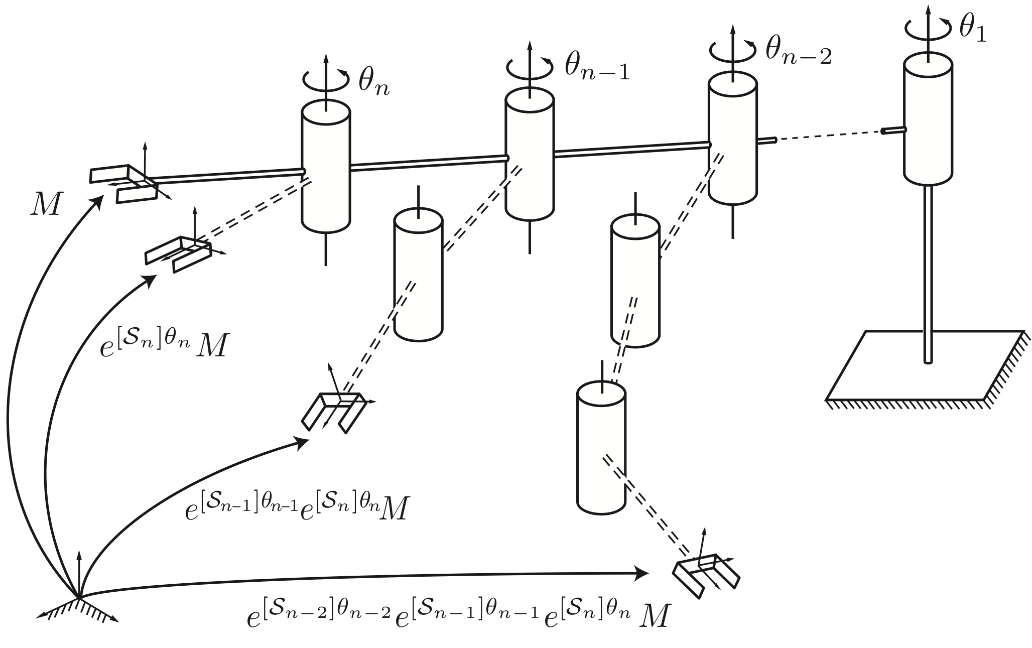
PoE（Product of Exponential）Formula $$ T_{sb}(\theta_1,...,\theta_n)=e^{[ e}\mathcal{S}_1]\theta_1^{[ ... e}\mathcal{S}_2]\theta_2^{[M $$}\mathcal{S}_n]\theta_n

1、所有$\theta = 0$,计算初始$M$ 2、从后往前，转动最后一个关节，其余关节为0 3、继续转动倒数第二关节，其余关节为0 4、。。。 5、按照screw motion计算，在计算PoE公式

步骤： 1. 建立坐标系（基坐标系${S}$，工具坐标系${T}$），只需要这两个坐标系，其他关节确定关节轴线或者移动方向即可。 2. 计算$\theta_1 = ...=\theta_n=0$时的初始位形，基坐标系与工具坐标系的$M$的变换${}_T^S{g(0)}$ 3. 计算$w_i$， 4. 关节轴线上的一个点，所以那个$r_i$并不固定，但是不影响计算结果。 5. 计算单位运动旋量$\xi_i=[w_i,r_i\times w_i]^T$（转动副），$\xi_i=[0, v_i]^T$（移动副） 6. 根据公式：$e^{\theta \hat\xi} = \begin{bmatrix} e^{\theta \hat w} & ({I}-e^{\theta \hat w})(w \times v) + \theta ww^Tv \\ 0 & 1 \end{bmatrix}$,$w \neq 0$ 7. ${}_T^S{g(\theta)}=e^{\theta_1 \hat\xi_1} e^{\theta_2 \hat\xi_2} \dots e^{\theta_i \hat\xi_i} \dots e^{\theta_n \hat\xi_n} {}_T^S{g(0)}$

7.4、练习题¶

2自由度机器人(RR)

P53

平面3自由度机器人(RRR)

P55

空间3自由度机器人(RRR)

解 1. 建立如下图所示的坐标系 2. SCARA机器人(RRRP)

P56

6自由度机器人(RRRRRR)

8、Inverse Kinematics¶

解析解的几种方法

9、Velocity Kinematics¶

deriving the Jacobian matrix:linearized map from the joint velocities $\dot \theta$ to the spatial velocity $\mathcal{V}$ of the end-effector

1、（重点） 空间雅可比（space Jacobian）,$J_s(\theta)$，简单理解为基于基坐标系的，或张巍老师讲的情况。公式如下： $$ J_s(\theta)=$$

2、物体雅可比（body Jacobian），$J_b(\theta)$，末端（物体）坐标形式下的雅可比矩阵。

10、Dynamics¶

11、旋量系、互异旋量系、运动旋量系、约束旋量系、等效运动副旋量系。。。¶

这部分内容偏机构学中的分析方法。